[BaekJoon] 백준 2263번 : 트리의 순회

2263번 : 트리의 순회

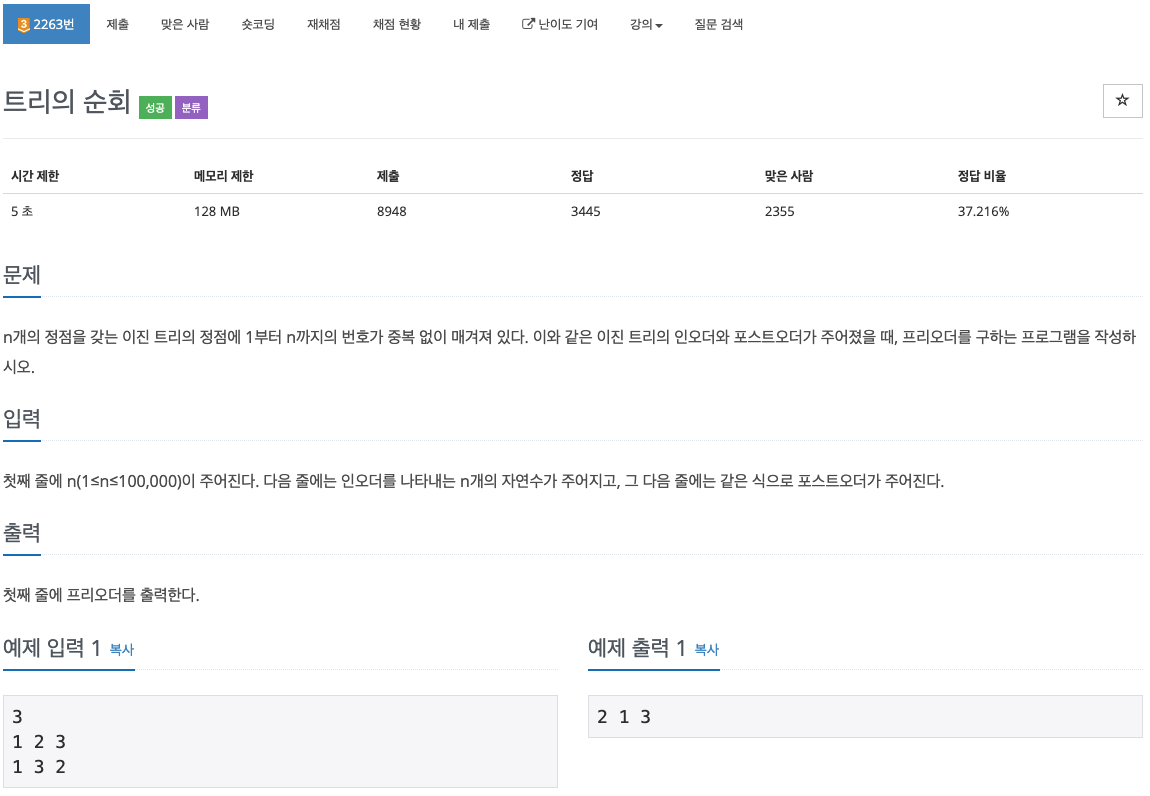
[BaekJoon] 백준 5639번 : 이진 검색 트리 문제와 매우 유사한 문제이다.

5639번 문제는 전위순회를 주고 후위순회를 구하는 문제였지만 이 문제는 중위, 후위 순회를 통해 전위 순회를 구하는 문제이다.

재귀를 통해 풀면 되겠다 싶어 처음 접근한 방법은

1. 후위 순회를 통해 루트 노드를 찾고 출력
2. 중위 순회에서 루트 노드를 기준으로 왼쪽 오른쪽 트리로 나눔
3. 왼쪽 오른쪽 트리 길이만큼 후위 순회를 자름
4. (중위 순회 왼쪽, 후위 순회 왼쪽), (중위 순회 오른쪽, 후위 순회 오른쪽) 재귀

import sys

sys.setrecursionlimit(10 ** 6)


def _solution(in_split, post_split):
	if len(in_split) <= 2:
		for val in reversed(in_split):
			print(val, end=" ")
		return

	root = post_split[-1]
	root_index = in_split.index(root)
	print(root, end=" ")

	in_order_left = in_split[:root_index]
	in_order_right = in_split[root_index + 1:]

	post_order_left = post_split[:len(in_order_left)]
	post_order_right = post_split[len(in_order_left):-1]

	_solution(in_order_left, post_order_left)
	_solution(in_order_right, post_order_right)


def solution():
	root = post_order[-1]
	root_index = in_order.index(root)
	print(root, end=" ")

	in_order_left = in_order[:root_index]
	in_order_right = in_order[root_index + 1:]

	post_order_left = post_order[:len(in_order_left)]
	post_order_right = post_order[len(in_order_left):-1]

	_solution(in_order_left, post_order_left)
	_solution(in_order_right, post_order_right)

	return


if __name__ == '__main__':
	n = int(input())
	in_order = list(map(int, sys.stdin.readline().rsplit()))
	post_order = list(map(int, sys.stdin.readline().rsplit()))

	solution()

이렇게 코드를 짠 뒤 제출을 했는데 메모리 초과가 발생했다.

이유를 검색해보니 파이썬은 slice 를 하는 경우 매번 새로운 리스트가 만들어져

너무 많은 리스트 때문에 메모리 초과가 발생한 것이었다.

질문 글을 검색해보니 재귀를 돌릴 때 매번 잘라서 넘기지 말고 잘라야 하는 인덱스만 넘기면 해결 할 수 있다고 했다.

잘라서 넘기면 이해하기가 편한데 인덱스로 넘기자니 이해가 너무 안가서 힘들었다..

또 루트 인덱스를 매번 찾는 방식으로 했더니 시간 초과가 발생해 루트 인덱스는 사전에 저장해두고 사용했다.

---

import sys

sys.setrecursionlimit(10 ** 6)


def solution(in_order_start, in_order_end, post_order_start, post_order_end):
	if in_order_start > in_order_end or post_order_start > post_order_end:
		return

	root = post_order[post_order_end]
	root_index = root_index_dict[root]
	print(root, end=" ")

	in_order_len = root_index - in_order_start
	# left
	solution(in_order_start, root_index - 1, post_order_start, post_order_start + in_order_len - 1)

	# right
	solution(root_index + 1, in_order_end, post_order_start + in_order_len, post_order_end - 1)


if __name__ == '__main__':
	n = int(input())
	in_order = list(map(int, sys.stdin.readline().rsplit()))
	post_order = list(map(int, sys.stdin.readline().rsplit()))
	root_index_dict = dict()
	for i in range(n):
		root_index_dict[in_order[i]] = i

	solution(0, n - 1, 0, n - 1)